Annual Percentage Rate (APR) tells you the nominal interest rate for a loan or investment but often hides an important detail: how often the interest is compounded. An investment or loan with monthly compounding yields more than one with annual compounding because each compounding period earns interest on previously accrued interest. To compare products accurately you need the Effective Annual Rate (EAR) – the true annual return or cost once compounding is factored in. APR and EAR may look similar, but they serve different purposes: APR expresses the nominal rate and may include fees, while EAR captures compounding and reflects the actual cost or return.
What Is EAR and Why Convert APR to EAR?
APR (Annual Percentage Rate) is the nominal annual rate lenders quote. It may include some fees and does not account for how often interest is capitalised. EAR (Effective Annual Rate) tells you the actual annual return or cost once compounding frequency is included. EAR is essential when:
- You want to compare two loans or investments with the same nominal APR but different compounding periods.
- You need to understand the true cost of borrowing or the actual yield on an investment.
For instance, a 12 % APR compounded monthly produces a higher yield than the same 12 % nominal rate compounded annually, because interest is earned on interest each month.
Formula for Converting APR to EAR
The relationship between APR and EAR is straightforward once you know the compounding periods. Let:
- i – the nominal interest rate (APR) as a decimal (e.g., 0.12 for 12 %).
- n – the number of compounding periods per year (e.g., 12 for monthly, 4 for quarterly).
The EAR is calculated using the compound interest formula: EAR=(1+in)n−1\text{EAR} = \left(1 + \frac{i}{n}\right)^{n} – 1EAR=(1+ni)n−1
This formula grows the nominal rate in equal compounding steps and subtracts one to obtain the effective rate. Once calculated, multiply by 100 to express EAR as a percentage.
Visualising APR vs. EAR
To understand why EAR is higher than APR when compounding is more frequent, it helps to see the difference. The bar chart below compares APR and EAR for a 12 % nominal rate with different compounding periods.
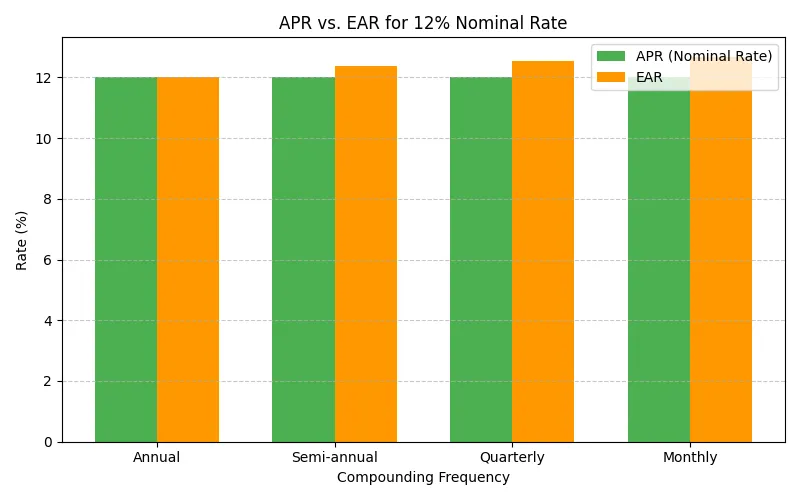
In the chart, the APR is a flat 12 % across all scenarios because it is simply the nominal rate. The EAR rises from 12 % (annual compounding) to around 12.68 % for monthly compounding. This illustrates how compounding frequency boosts the effective return.
Step‑by‑Step: How to Convert APR to EAR
Follow these simple steps to convert an APR into its effective annual rate:
- Identify the APR and compounding frequency. For example, an APR of 12 % compounded monthly means i = 0.12 and n = 12.
- Convert the APR to a decimal and divide by the number of compounding periods: i/n. For our example, 0.12/12 = 0.01.
- Add 1 and raise to the power of n: (1+i/n)n(1 + i/n)^{n}(1+i/n)n. The factor in our example is (1+0.01)12(1 + 0.01)^{12}(1+0.01)12.
- Subtract 1 to find the EAR in decimal form, then multiply by 100 to convert to a percentage. The result of (1+0.01)12−1(1 + 0.01)^{12} – 1(1+0.01)12−1 is about 0.1268 or 12.68 %.
The flowchart below summarises these steps visually.
Worked Example
Let’s apply the method to a 12 % APR with quarterly compounding (n = 4):
- APR (i) = 12 % → 0.12 as a decimal. Compounding periods (n) = 4.
- Divide the APR by n: 0.12/4 = 0.03.
- Add 1 and raise to the power of 4: (1+0.03)4=1.034=1.1255(1 + 0.03)^4 = 1.03^4 = 1.1255(1+0.03)4=1.034=1.1255.
- Subtract 1: 1.1255 – 1 = 0.1255 or 12.55 %. The APR of 12 % becomes an EAR of about 12.55 % under quarterly compounding.
How EAR Changes with Compounding Frequency
Another way to grasp how compounding influences effective returns is to look at how the EAR climbs as the number of compounding periods increases. The chart below plots the EAR for a 12 % nominal rate across a wide range of compounding frequencies, from annual (1) to daily (365).
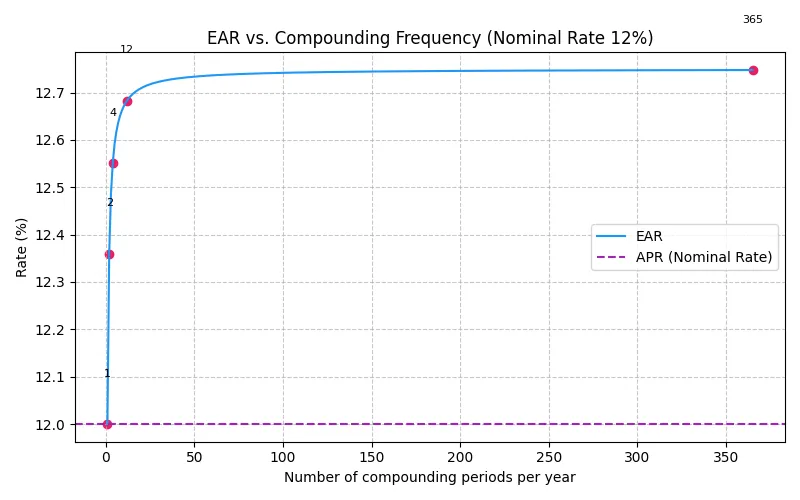
Notice how the curve climbs steeply when moving from annual to semi‑annual and quarterly compounding, then starts to flatten as compounding becomes more frequent. Continuous compounding yields the highest possible EAR, but the gains diminish as n grows.
When to Use APR vs. EAR
Although they are related, APR and EAR serve different rolesdaytrading.com:
- APR is useful for quoting loan rates and comparing products that include fees. It is a standardised way to express nominal interest and allows consumers to compare loans with similar compounding structures.
- EAR is ideal for evaluating the true return on investments or the actual cost of borrowing when interest is compounded more often than annually. It is particularly important for high‑frequency compounding, such as credit cards or savings accounts.
If you want to know how much you will actually pay or earn, convert the APR to EAR.
Final Thoughts
Understanding how to convert APR to EAR empowers you to make better financial decisions. The process is straightforward: divide the nominal rate by the number of compounding periods, apply the compound interest formula, and convert back to a percentage. Use the APR to EAR conversion whenever compounding frequency matters – for example, when comparing savings accounts, credit cards, or investment products with different compounding intervals. With the help of visual aids and a simple formula, you can demystify effective annual rates and ensure you’re comparing apples to apples in the world of finance.